A while ago I was studying the webp image format by Google out of curiosity. I had written a .png parser in the past and was interested in seeing how the lossless VP8L encoding in particular was working in that library.
While I was using a external Rust library to decode the actual image data in the past, I quickly found myself drawn to trying to implement the decoding myself. Long story short, after several days of trying to wrap my head around their Huffman decoding optimization I had to give up. I just couldn’t understand how it worked.
I moved on, but I couldn’t get the problem out of my head. Only several weeks later, while doing something completely unrelated to programming, it suddenly all clicked into place. Since I still haven’t found a good article that explains it, I’m here now to explain how the Huffman-Coding lookup table works.
But let’s start at the beginning: what even is a Huffman-Coding and what is this optimization I was talking about?
Introduction to Huffman Coding
If you learned about the basics of this algorithm in college, like I did, feel free to skip this section. If you’ve never even heard of this, or if it’s been a while and you want a refresher, keep reading.
According to Wikipedia:
In computer science and information theory, a Huffman code is a particular type of optimal prefix code that is commonly used for lossless data compression. The process of finding or using such a code is Huffman coding, an algorithm developed by David A. Huffman while he was a Sc.D. student at MIT, and published in the 1952 paper “A Method for the Construction of Minimum-Redundancy Codes”.
For normal people: Huffman coding is a (very old in CS timelines) method to encode data more efficiently. It does this by assigning shorter codes to more frequent values, and longer ones to less frequent values. In aggregate, the resulting encoded string is shorter than the initial one, approaching the theoretical minimum size defined by the data’s entropy.
A prefix code in this context just means that there are no control characters in the final string. No code is a prefix of any other code, so the decoder can always uniquely identify each symbol as it reads the bits.
To compress a text with Huffman Coding, we first have to create a Huffman tree, by counting the frequency of each character and then aggregating it into a tree that’s approximately balanced according to their frequency. Once you’ve associated a count with each character, we take the characters with the lowest counts and join them into a tree, inserting the sum of the counts as the new root node. We then continue this, until all characters are inserted into the tree.
This works to compress the data because we are using longer codes for less frequent bytes and shorter codes for more frequent ones. So if a byte appears often, it will get compressed more efficiently, while bytes that are very rare can actually get longer. But since they appear so infrequently, we balance that overhead out with the space saved by or more frequent codes.
As an example, let’s take the string aaaaaaaabbbbbbccccddd. It contains eight a’s, six b’s, four c’s and three d’s. So our initial nodes are just those four. For our first step, we see that c and d have the lowest counts, so we group them into a new node by adding a parent:
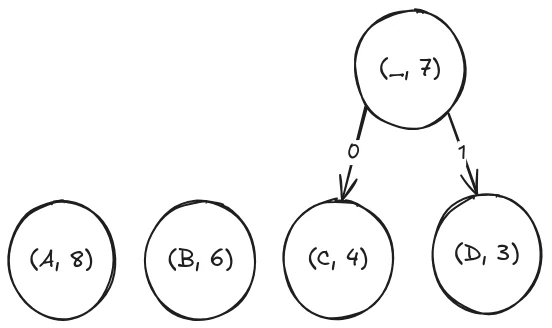
Next up, we see that the new c-d node and the b node are the smallest, so once again, we merge them into a single node:
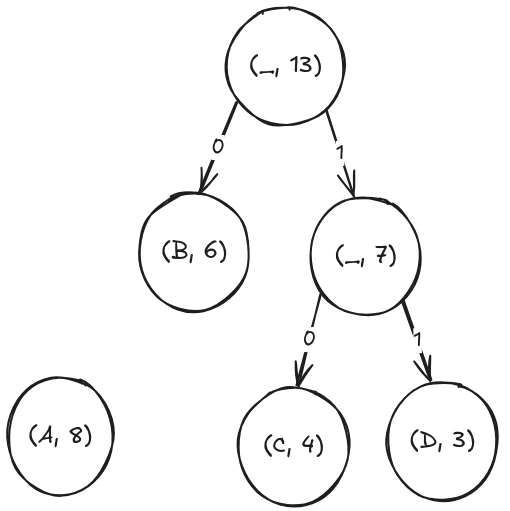
Now only two nodes are left, so in the last merge we create our final Huffman tree:
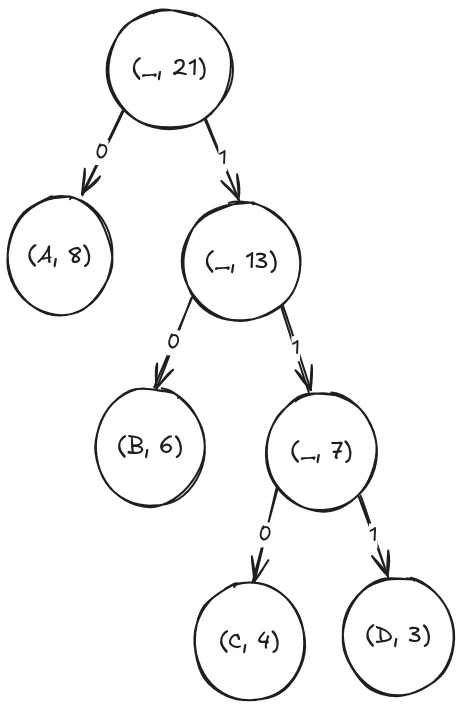
As you can see, I’ve also already annotated the prefix of each character. To save an a into our new string, it now only needs a single bit, a 0. To encode a b it’s 10 and c and d are 110 and 111. In total that would be 8 bits for the a’s, 12 bits for the b’s and 21 bits for the c’s and d’s, leaving us with 41 bits or 6 bytes in total, much shorter than the initial 21 bytes.
Decoding the Huffman Encoding
To decode the compressed string, we can just walk the tree in reverse, treating it as a decision tree. We start from the root, and for each bit we step one node down. If we hit a leaf node (one that contains a character), we write that character to our output buffer and jump back up to the root to start the next code.
Now while this is efficient to store, it’s not that efficient to decode: walking a tree requires many random accesses to memory and if statements. Both are not ideal for modern CPUs that try to predict our next moves to pre-fetch instructions and memory.
Every if statement is a chance for the CPU to miss-predict, and thus have to flush and re-fetch the instruction cache, throwing away the speculatively pre-computed result. Every jump to the next node risks the memory being flushed out of the CPU cache and thus then need to be fetched from a higher cache or, even worse, from RAM.
So we want to do as few memory operations as possible. Preferably just pick the result from a memory location and immediately continue decoding the input string.
That’s where the Huffman table comes into play. In contrast to the Huffman tree, the table is just a contiguous slice of memory, easily accessible. But we need to do some pre-computation to produce the table from the tree.
The Huffman Table Optimization
Since the Huffman coding guarantees that no code is a prefix of another, we can use that to our advantage. To start, we need to find the greatest code length (in bits) in the whole tree. In our case, that would be three, for both c and d.
Next, we traverse the tree, and for every node that has not yet reached that depth, we push it down to both of its children. To still know the initial length, we will also store the code length together with the decoded character.
Once we’re done with that procedure, we have a tree that’s completely full, all possible nodes are at the same level:
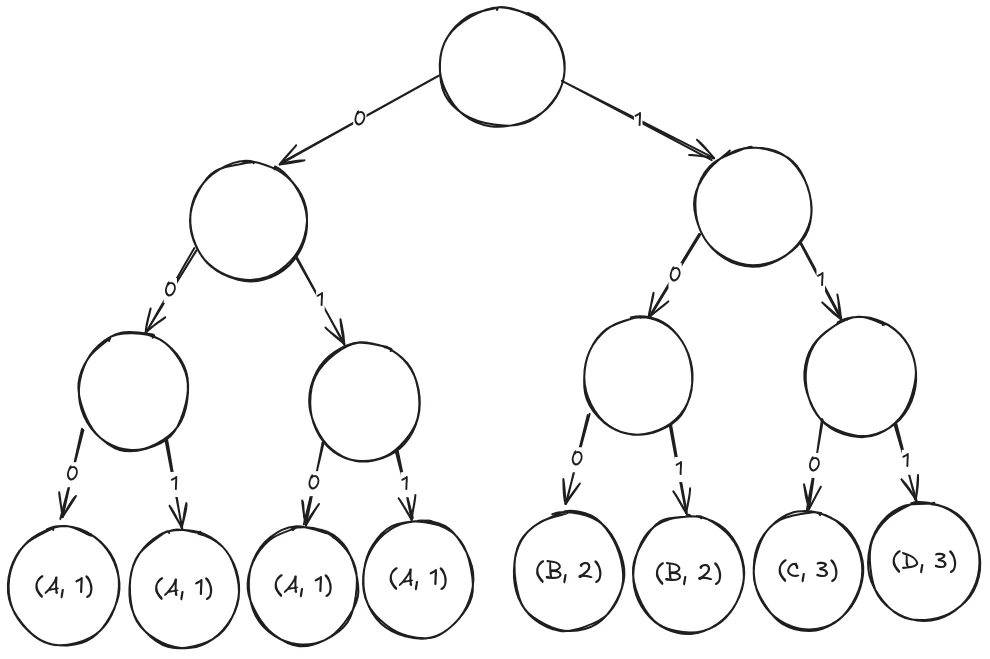
So how does this help us go forward? We now have more branches in the tree, with more jumps through memory and more possibilities for the CPU’s speculative execution to go wrong.
In fact, our tree now has O(2^n) leaf nodes, using much more memory in the process as well. Well, as we can see in this tree, at every node, whichever branch we take, we will always find ourselves in a valid branch, until we hit the tree’s depth. In other words, every bit-pattern of length n is valid in this search tree.
If you take a closer look at the leaf nodes, the first leaf node from the left can be accessed with the bit-pattern 000, the next with 001 and the one after that with 010 until we reach the last one with 111. What we did here is simply to create a lookup table for the prefix of the encoding.
So what we can do here is to simply discard the rest of the tree. Instead of taking the branches every time, we simply list the leaf nodes in a chunk of contiguous memory and then take the next n bit from the stream and index directly into it with a single operation, completely eliminating the need to traverse a tree.
Once we have our character and prefix code length, we can write the character to the output buffer and re-use the rest of the index that is longer than the prefix length.
Now, some of you may wonder if using O(n^2) memory is really any kind of optimization at all. And to that I can clearly say NO. In the worst case, if we are encoding single bytes, we will end up with 2^256 bytes of memory usage, which is far more memory than humanity has produced so far.
But Google was aware of that limitation as well when they produced the webp image standard. So they capped the total tree depth to at most 19, which would use 1MiB of RAM for the lookup table, maintaining a good trade-off between encoding efficiency and memory usage during decoding.
In summary, Huffman coding is a cool way to compress data, and the lookup table optimization makes decoding much faster, at the cost of some extra memory. This helps us improve decoding times, especially for lower-end devices, as we are repeating the same steps sometimes multiple times per pixel in image decoding.
These Solutions are Engineered by Humans
Did you find this article interesting? Does it match your skill set? Programming is at the heart of how we develop customized solutions. In fact, we’re currently hiring for roles just like this and others here at Würth IT Italy.






